从一个自称 Go 最快排序说起
从一个自称 Go 最快排序说起
本次的分享主题来源于一条朋友圈,标题就是最快的排序。这个标题特别吸引我的注意,本着这个排序到底是个什么玩意儿的心态点了进去,得到的有效信息其实不多(其实只得到了这个排序叫 pdqsort 在 Go 语言中是最快的)。我想都不用想,一猜就肯定在吹牛,凭什么他说最快就最快。之前在上数据结构课程的时候对于一些基本的排序还是有一定的了解的,对于这些排序也都是采用过不小的数据集进行测试过的,我完全接受不了说那种排序是最快的这种话的!!!!

简述
通过查询资料得知 pdqsort 是一个混合排序算法,对于这个混合排序我了解的不多,于是我打开了我的搜索引擎,输入了“混合排序的介绍”。。。。以下是我查询到的一些资料
Go、Rust、C ++ 的默认排序算法虽然名义上叫快速排序(quicksort),但其实质是混合排序算法(hybrid sorting algorithm),它们虽然在大部分情况下会使用快速排序算法,但是也会在不同情况下切换到其他排序算法。”涨知识了“,我一直以为他们就是在课本上学习的快速排序而已。。。

混合排序
一般来说,常见的混合排序算法,都会在元素较少(这个值一般是 16 ~ 32)的序列中切换成插入排序(insertion sort),在其他情况下,默认使用快速排序算法。
然而,快速排序算法有可能因为 pivot 选择的问题(有些序列 pivot 选择不好,导致性能下降很快)而导致在某些情况下可能到达最坏的时间复杂度 O(n^2),为了保证快速排序算法部分在最坏情况下,我们的时间复杂度仍然为 O(n* logn),所以在特定的条件下会转换成其他的排序。
用一句话来说“目前流行的混合排序算法基本都是在不同的情况,使用不同的方式排序来达到最优解”。

按照上面的解释我好像可以理解一点号称最快了,毕竟可以通过不同的序列变换不同的排序方式。根据不同的序列不断的变换排序方法确实可以在理论上达到最优解,但是,我对于这个还是持怀疑的态度,根据一个序列选择最优的排序方法,这个也太难了吧!!!

前置
带着上面的怀疑我开始了搜索大法,最后搜索到了一篇论述 pdqsort 的论文。论文中解释了 pdqsort 是一个基于插入排序、堆排序和快速排序所组合的排序。论文地址:https://arxiv.org/pdf/2106.05123.pdf
我相信大家对于上述的排序都是知道的,我下面就简单的介绍一下,帮大家在回忆一下吧。

插入排序
排序过程
- 从第一个元素开始,认为第一个元素已经被排序
- 取出下一个元素,在已排好序的序列中从后往前扫描
- 如果该元素(已排好序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排好序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2-5
动图介绍
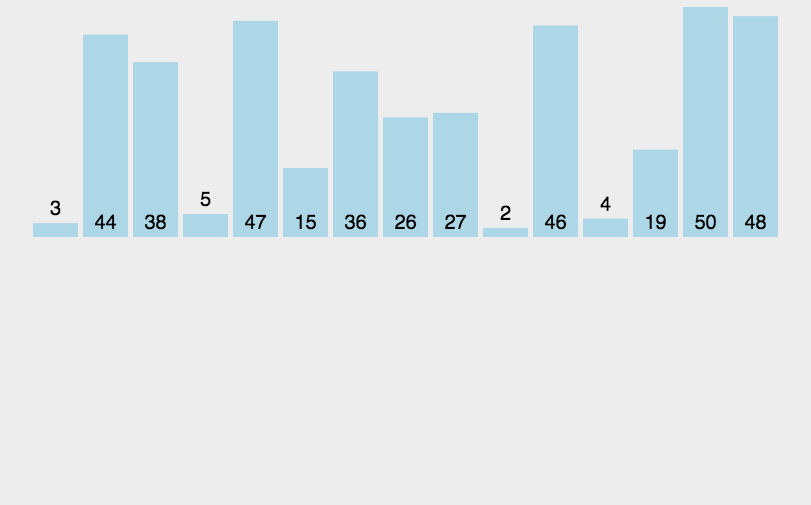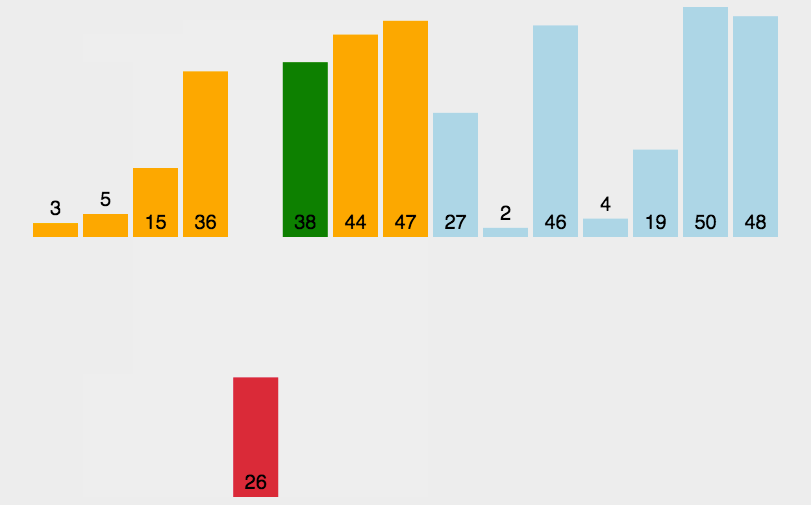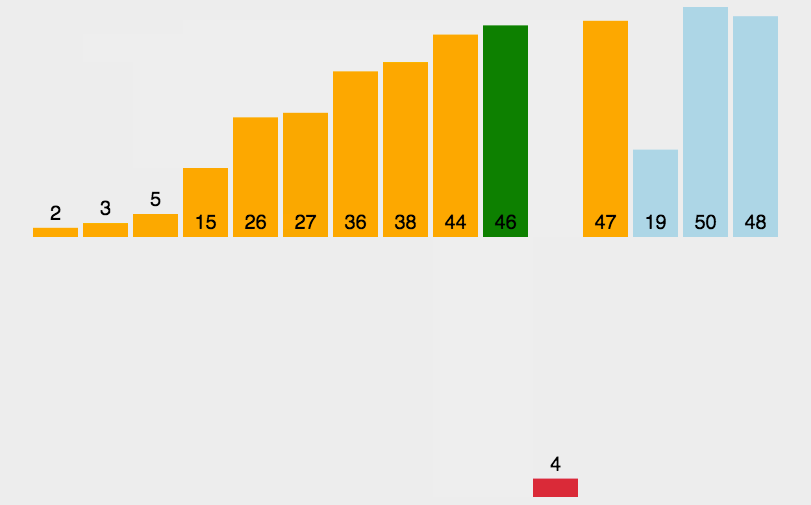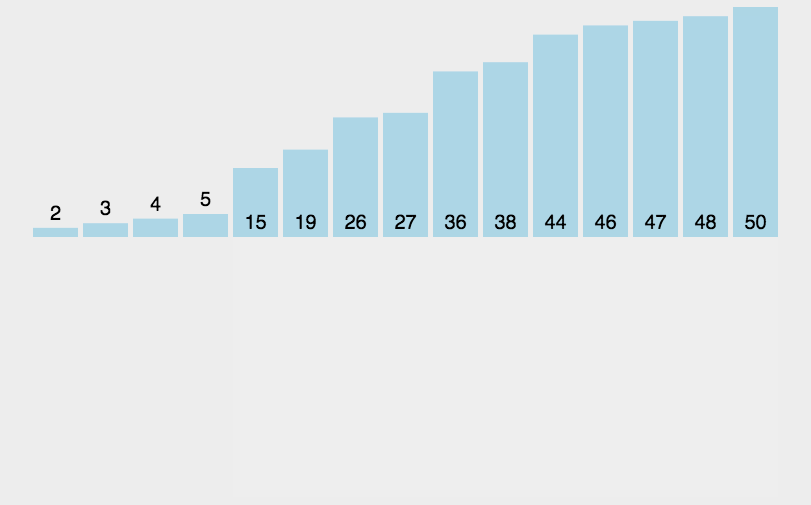
堆排序
排序过程
- 将待排序的元素构建成一个二叉堆。首先将所有元素插入到一个数组中,然后从最后一个非叶子节点开始,向下调整堆的结构,使得每个节点的值都大于或等于其子节点的值(对于大根堆)或小于或等于其子节点的值(对于小根堆)。
- 取出堆的根节点,即堆中最大的元素,并将其放到数组的末尾。
- 将剩余的元素重新构建成一个堆,方法是将根节点的值替换为最后一个元素,然后从最后一个非叶子节点开始,向下调整堆的结构。
- 重复步骤2和步骤3,直到所有元素都被排序。
动图介绍

快速排序
排序过程
快速排序使用分治算法来把一个序列分为两个子序列,具体算法描述如下:
\1. 从序列中选择最右边的数作为基准,称为 “基准值”(pivot);
\2. 遍历排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面;
\3. 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
动图介绍
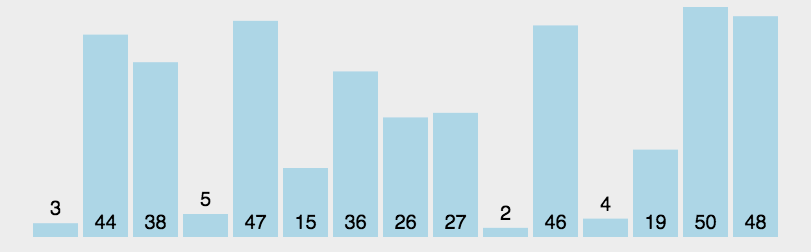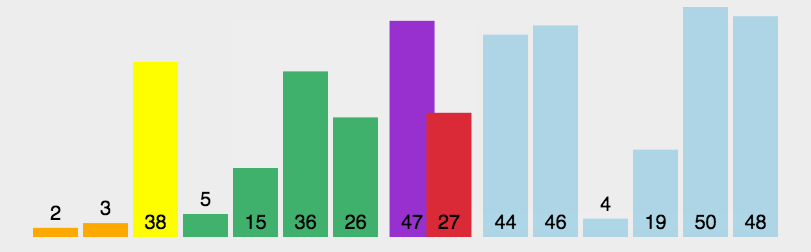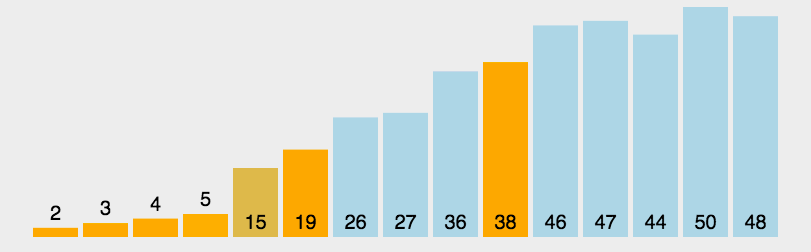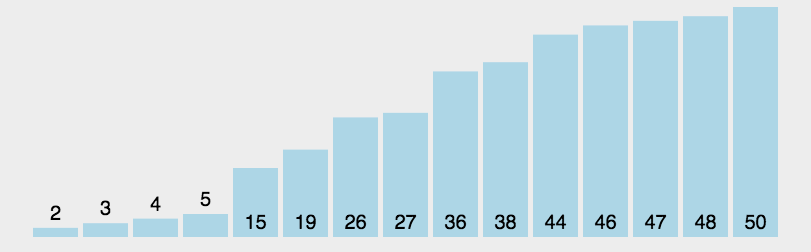
性能对比
时间复杂度
| 最好情况 | 一般情况 | 最坏情况 | |
|---|---|---|---|
| 插入排序 | O(n) | O(n^2) | O(n^2) |
| 堆排序 | O(n*logn) | O(n*logn) | O(n*logn) |
| 快速排序 | O(n*logn) | O(n*logn) | O(n^2) |
https://www.jianshu.com/p/958b346130b9
看完上面这篇文章其实结论就一个,当数据量比较小的时候插入排序是性能最好的(其实我有点不理解哈)
综合性能来看快速排序是最好的,堆排序和归并排序是比较稳定的。
pdqsort(go)实现分析
项目地址:https://github.com/zhangyunhao116/pdqsort
本来都按照项目代码直接进行分析了,后面看到了这个排序方法的开发者发表的一篇文章。其中讲述了开发过程中不断优化的过程,我觉得一步步优化的过程比较有意思,所以这一章节直接重新写了一遍。
初步构思
上面对于一些基础排序也是进行了分析,也了解了 qdqsort 是有插入排序、堆排序和快速排序混合组成的。既然它是通过混合上述几种排序所组成的,那么肯定是要集成这几种排序的优点,进行一个扬长避短。
思路如下:
- 通过 Benchmark 测试结果可以看出,对于短序列的排序使用插入排序是最快的,则可以对序列长度判断
当序列长度在一个区间时,采用插入排序。
- 非短序列的情况来看快速排序的综合性能比较高,对于非短序列则使用快速排序
- 根据理论分析结果来看快速排序在基准值值比较差的时候,时间复杂度有可能会达到 O(n^2),采用堆排序保底,以至于不会过于的慢。
按照上述思路来看,我们需要确定两个东西:什么长度的序列叫做短序列?什么情况快速排序会转变成堆排序?
看了一下项目代码,对于短序列的长度规定为小于等于 24。
当选择的基准值进行第一次排序时,发现基准值的位置小于 bits.Len(length) 时认定快速排序效果不佳,即转换为堆排序。流程图如下:
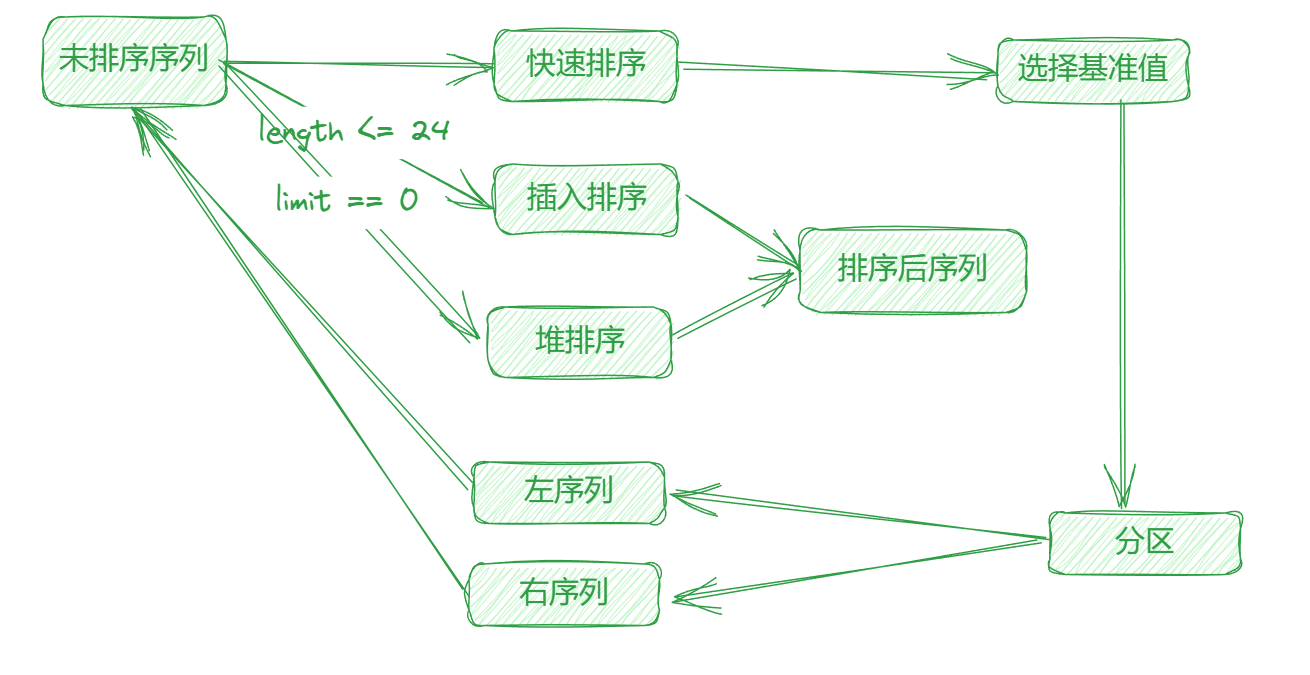
初步优化
按照在课本上学习的快速排序来看基准值一般都是选择第一个数据为基准值的。但是,我们知道基准值为中位数的时候才是最优的选择。当我们真的选择真正的中位数的时候,基本上只有一个方法那就是 —> 遍历序列。想都不用想这个方式时不可行的。那我们只能退而求其次选取一个近似中位数。
选择近似中位数方案如下:
- 短序列(<= 8)选取第一个元素
- 中序列(<=50) median of three
- 长序列(> 50) median of medians
median of three
这个方法是分别取最左边、最右边、中间三个值,然后选出其中间值作为 pivot。例如 [4,3,2,1],我们会选取 4 3 1 然后选择其中的 3 作为 pivot。这种方式相比于首个元素的方式会更加合理,因为采样了多个元素,不容易受到一些极端情况的影响,往往会比首个元素的方式有更好的效果。
stackoverflow discussion:
https://stackoverflow.com/questions/7559608/median-of-three-values-strategy
median of medians
这个方法的原理其实和 median of three 相似,不同的地方在于加大了 pivot 的采样范围,在 array 长度较长的情况下理论表现会更好。其采样步骤是先将 array 分为 n/5 个 sub-arrays,n 为 array 的长度。然后将这些 sub-arrays 的 medians 都取出,选取这些 medians 中的 median,同样的方式如此反复,最后得到一个 median of medians 作为最后的 pivot。
stackoverflow discussion:
https://stackoverflow.com/questions/5605916/quick-sort-median-selection
Median-finding Algorithm:
https://brilliant.org/wiki/median-finding-algorithm/#citation-1
采样数据反正都采样了不能只用于选择基准值呀,于是就有了下述的优化方案
- 采样元素为逆序,推测系列已经是逆序,revers 学列
- 采样元素为顺序,推测序列已经是顺序,使用插入排序
使用插入排序的时候,我们不能无脑的一直插入排序到排序完成,所以需要限制一下排序次数
流程图如下:
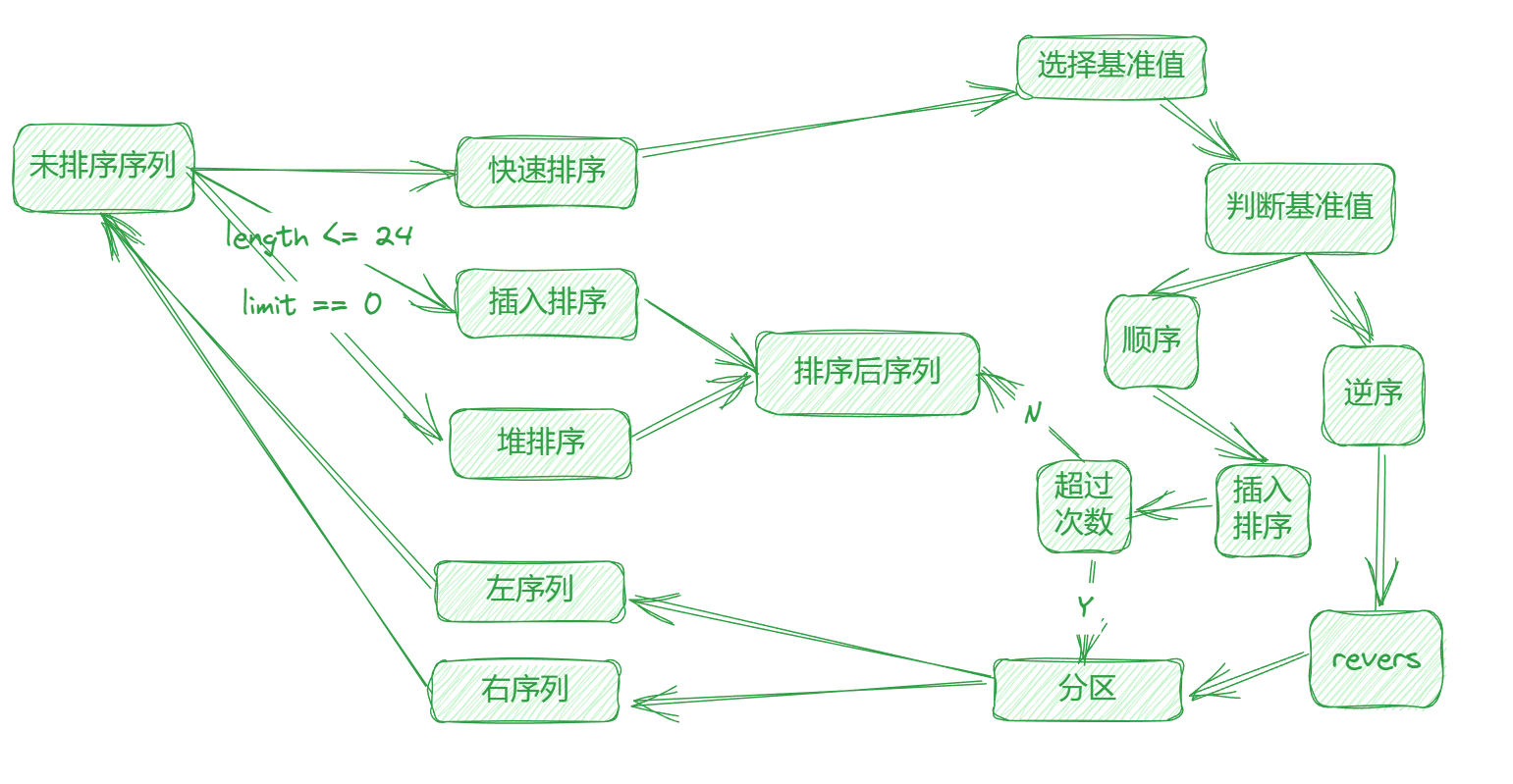
最终优化
我们都知道快速排序是有可能交换相同元素的,所以当一个序列重复度比较高的时候,快速排序效率会比较低。
跟选择中位数一样,我们不能通过遍历去获取判断结果,所以也只能从采样元素入手。
如果两次分区的基准值相同的时候,按照快速排序的原理,可以知道知道这两次的排序其实是重复的,没必要都执行的。所以当前基准值和上一次的基准值是一致的情况下使用 partitionEqual 函数将重复元素排列到一起,这样就可以有效的解决无效分区的情况。流程图如下:
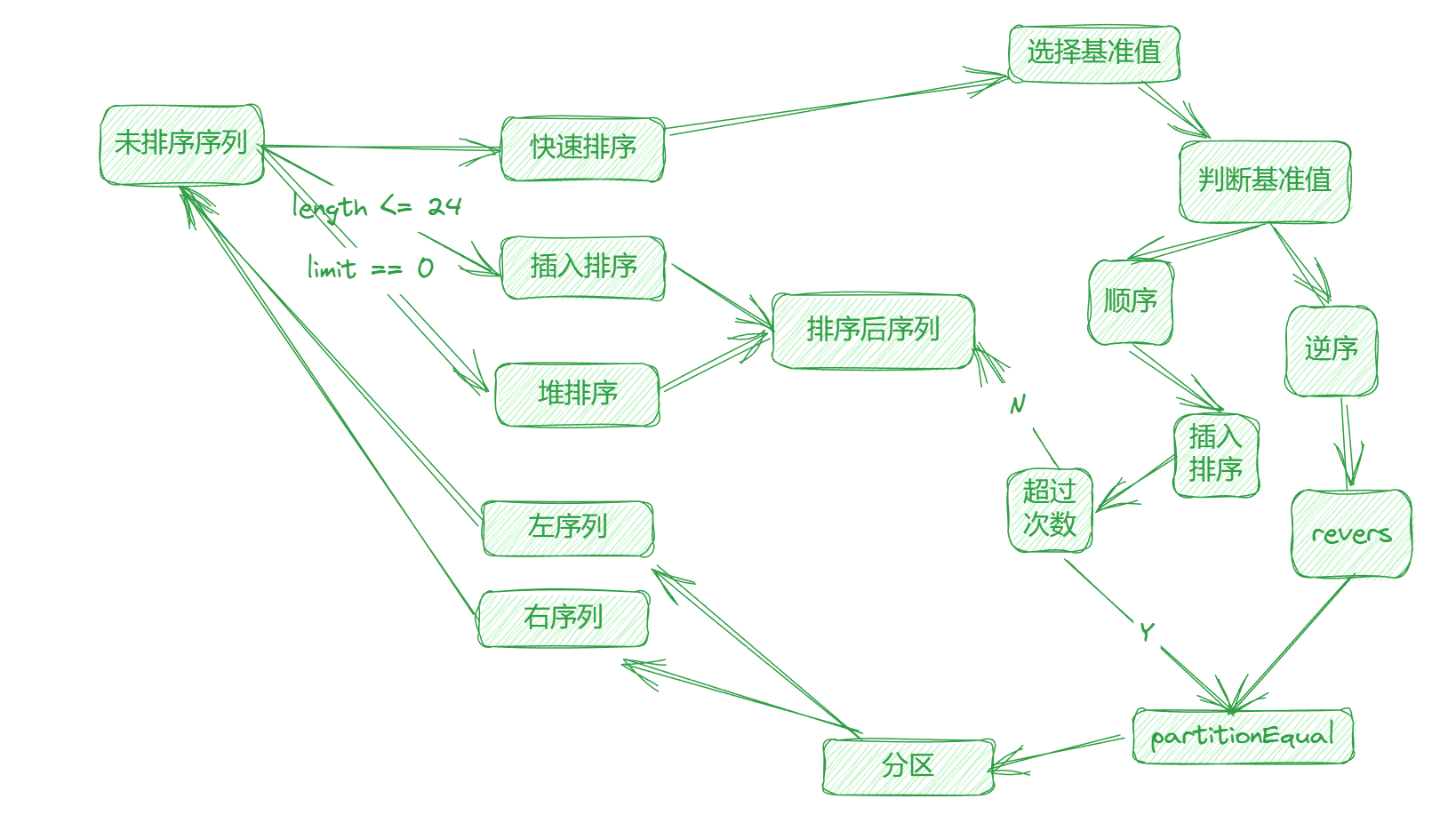
杂述
go pdqsort benchmark 测试结果 https://github.com/zhangyunhao116/pdqsort#benchmark
go pdqsort 已经是 go 官方所默认的排序了 https://github.com/golang/go/issues/50154
Go 原有的算法类似于 introsort,其通过递归次数来决定是否切换到 fall back 算法,而 pdqsort 使用了另一种计算方式(基于序列长度),使得切换到 fall back 算法的时机更加合理。
在纯粹的算法层面,即 pdqsort (with sort.Interface) ,pdqsort 在完全随机的情况下和原有算法(类似于 IntroSort)性能几乎一致。在常见的场景下(例如序列有序|几乎有序|逆序|几乎逆序|重复元素较多)等情况下,会比原有的算法快 1~30 倍。
参考
https://github.com/golang/go/issues/50154
https://zhuanlan.zhihu.com/p/506017637